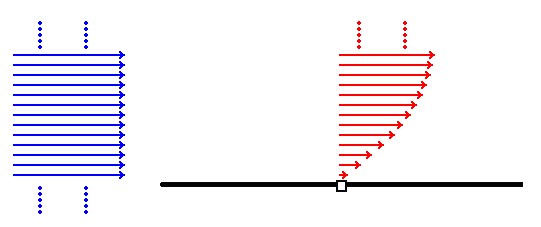
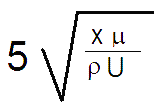Case studiesBoundary layersIt may seem strange to call a gas a fluid but, mathematically speaking, a moving gas has many similarities with a moving liquid. The study of flowing fluids is the subject of fluid mechanics and when a fluid moves over a solid surface a boundary layer arises. Fluids have viscosity. This is readily apparent in a very sticky fluid such as honey, You can see that honey tends to stick to itself as well as to any jar from which you're trying to pour it. Air is viscous as well, though much less so than honey, and also tends to stick to itself and to any surface it is in contact with. For any fluid in contact with a solid surface, the velocity of the fluid at the fluid-solid interface is the same as that of the solid. This is called the no-slip condition. The no-slip condition has some every-day consequences for it is part of the reason why dust accumulates on fan blades. Consider the following diagram, which shows a fluid flowing over a stationary black plate aligned parallel to the fluid flow.
Before it reaches the plate the fluid is flowing uniformly. The equal length blue arrows on the left indicate that throughout its depth the fluid is moving at the same velocity and the dots indicate that there's much more fluid above and below. Call the velocity indicated by the blue arrows the free-stream velocity Now consider the point on the plate marked by the white square. The red arrows show a range of velocities (or a velocity gradient) within the fluid above that particular point. The longer the arrow the greater the magnitude of the velocity. Because of the no-slip condition the fluid in contact with the plate is still but well away from the plate the fluid is moving with the free-stream velocity. In between there is a range of velocities. Very close to the plate there is a low velocity, a little further away the velocity is a little greater, a little further away still the velocity is a little greater still and so on. Above the plate each point in the fluid has its own local velocity. If you joined up the tips of the arrowheads with a line you'd get a curve that you could call the shape of the velocity gradient for the point marked with the white square. In this scenario there's nothing special about the area above the plate. Below the plate you'd have a mirror image of what's happening above the plate. Velocity gradients are associated with the term boundary layer. Steven Vogel, one of whose books is the source of much of the information on this page, has written the following in the introduction to chapter 8 of that book:
Close to a solid surface fluid viscosity has various significant effects and it would seem reasonable to differentiate such a region. But what is significant? The velocities increase gradually and continuously from zero and there is no point above the plate where viscosity effects suddenly change from significant to insignificant. There is therefore no natural upper break and it is necessary to make an arbitrary decision. The outer limit of the boundary layer is commonly defined as made up of all those points in the fluid where the local velocities are 99% of the free-stream velocity. Using this definition and making some reasonable assumptions gives the following as an approximate formula for the height of the boundary layer above the plate at a given point: where the symbols under the square root sign have the following meanings:
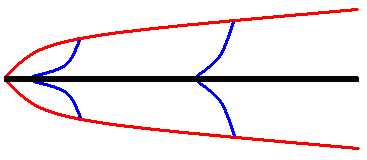
Given that X and µ are above the line, the larger these values are the greater the thickness of the boundary layer. On the other hand, since ρ and U are below the line, the larger these values are the smaller the thickness of the boundary layer. So, all other things being equal, the more viscous the fluid the thicker the boundary layer. For any given fluid and free-stream velocity, the further away from the leading edge of the plate, the thicker the boundary layer. In fact at the leading edge (where X has the value 0) the boundary layer has zero thickness. The red lines in the next diagram give you an idea of the shape of a boundary layer produced by the formula given above. The vertical distances are much exaggerated, given the size of the plate, but the diagram is qualitatively useful. You see that the boundary layer is steep near the plate's leading edge but less so downstream. The blue lines show the shapes of the velocity gradients at two points along the plate. The further downstream the "flatter" the velocity gradient curves become. Some warningsYou'll occasionally see boundary layers referred to as areas where the air is still. As you can see that's not necessarily the case. Rather, they are zones where the effects of viscosity are significant. Strictly speaking it's even a little misleading to talk of THE boundary layer for a particular scenario. The use of the 99% factor in the definition above is very common but it is worth noting that some other definitions are in use. Depending on what viscosity-induced aspects you are studying you may find another definition far more useful for separating the "viscous" from the "non-viscous" regions. It's clear that the flat-plate scenario is simplistic - the real world is a much more complex place. Nevertheless the flat-plate scenario has an educational value. It allows an easy explanation of the development of velocity gradients from the no-slip condition and the derivation of a formula for the shape of a boundary layer. That in turn shows how some parameters influence boundary layers. The above discussion has been about laminar boundary layers where there is smooth flow over the surface. That's sufficient for this bryophyte website. There are also turbulent boundary layers, which are much more complex. Finally, the discussion has assumed that the fluids are "everyday" fluids, such as air or water, in the various habitats that cover the earth's surface. There are more esoteric fluids (for example, very low density gases) or environments (such as very high altitudes) for which not all the above comments hold. Bryophytes and boundary layersBoundary layers are highly significant for small organisms that live their lives on surfaces since such organisms spend much of their time living within the boundary layers of some surface or other. Many bryophytes are low-growing turfs, carpets, sheets or cushions. Very slow moving air is a good insulator and is also good at slowing the diffusion of molecules. Water that evaporates from a moist surface moves only slowly through the neighbouring boundary layer, thereby creating an ideal humid zone for any nearby bryophyte. Think of a rotting log on which some bryophytes are growing. The fungi that are rotting the log are breaking down complex organic molecules and releasing carbon dioxide. In the boundary layer over the log, given the slow diffusion of carbon dioxide, the carbon dioxide concentration can be much higher than that of the ambient air, giving the bryophytes an enhanced supply of the raw material of photosynthesis. Boundary layers are clearly helpful to bryophytes but they also create hurdles that need to be overcome. If spores are to be wind-dispersed there's no point releasing them into the boundary layer, for they'd go virtually nowhere. It is necessary to get the spores into the turbulent or faster moving air. So spore capsules need to be raised high enough to be clear of the boundary layer. References
|
![An Australian Government Initiative [logo]](/images/austgovt_brown_90px.gif)